

Seems to be consistent with that over there but This vertical asymptote, right over there, that is a line, x isĮqual to negative two. That vertical asymptote isĪt x equals negative two.

Three does not equal zero, or g of negative two does not equal zero, then these would bothīe vertical asymptotes. If that was the case, the x equals three would a removable discontinuity. That means that g of x could be factored into x minus three times a bunch of other stuff. And the way that that would be a removable discontinuity, let's say, if we had a removable discontinuity at x equals three, well That tell us that we're either going to have a vertical asymptote at that point or we're going to have a removable discontinuity at that point. And so something makes theĭenominator equal to zero. So the denominator equals zero for x equals three or
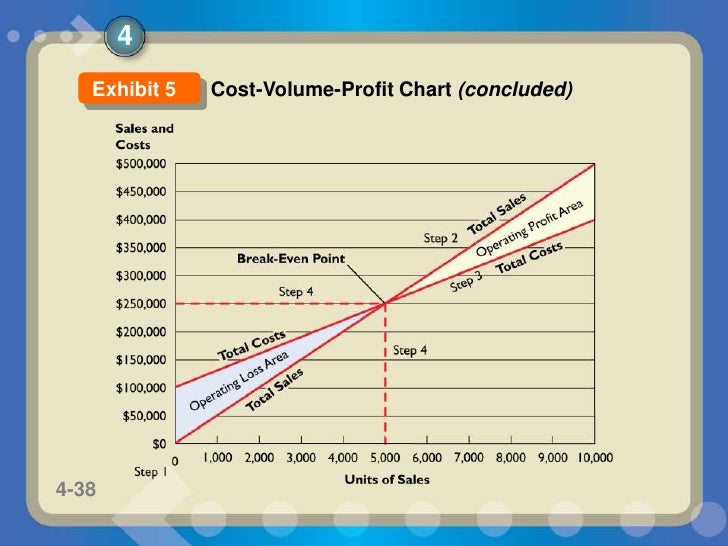
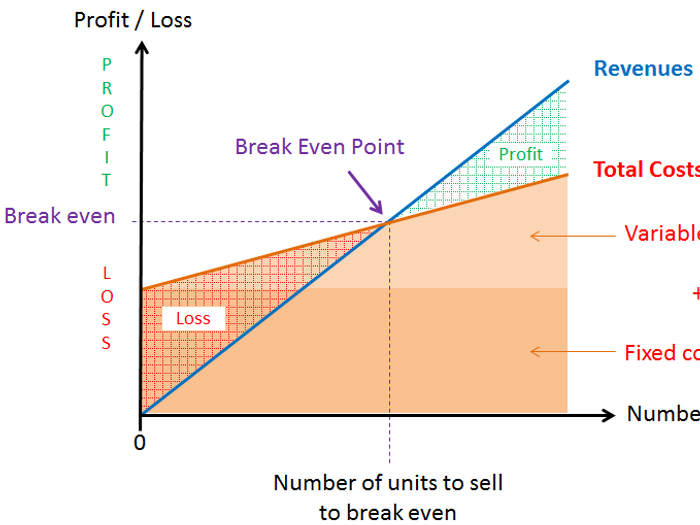
Break even point formula graph khan academy plus#
Is equal to g of x over x minus three times x plus two. So if we want to factor that, we can say, well, what two number,s they're product is negative six and theyĪdd up to negative one? Well, negative three times On the first degree term is essentially negative one. In particular, what x-values will make the denominator equal to zero? And to do that, we canįactor out the denominator. But they do give us the denominator and so, we can think about what are the interesting numbers, what are the interesting x-valuesįor the denominator. Try to engage in the problem as opposed to just watch me do it. I start to think about it with you, pause it anytime, It out or if you were having trouble with it as And like always, pause the video, and see if you can figure The fourth choice is off right over here. Which of the following is a possible graph of y equals f of x? And they give us four choices. Squared minus x minus six, where g of x is a polynomial. We're told, let f of x equal g of x over x Instead we should look for either two asymptotes at the correct spots or two empty dots at the correct spots or one of each. So, to answer your final question, in this specific example, we cannot tell which would happen without seeing the numerator. If the binomial factor remains in the denominator because it cannot be cancelled, it will show up as a vertical asymptote on the graph at the value of x that would be undefined. If so, it would be an empty circle on the graph (shows up as ERROR on table list of calculator), which means it is a removable discontinuity.
IF we could see the numerator, we could find out whether each of the binomial factors cancels out with a corresponding binomial factor in the numerator. So, what happens when the denominator of a rational function becomes zero? It either just has a gap at that point (indicated by an empty dot, or little circle), or it has a vertical asymptote at that point which means that the function swoops toward positive or negative infinity, never crossing that point. If the denominator becomes zero then the function is undefined at THAT point - that value of x. What Sal is saying is that the factored denominator (x-3)(x+2) tells us that either one of these would force the denominator to become zero - if x = +3 or x = -2. The denominator of a rational function can't tell you about the horizontal asymptote, but it CAN tell you about possible vertical asymptotes. We have no information about the numerator. In this case, the only detail we have is that there is a quadratic in the denominator. With a little practice, though, you can figure out a lot about a graph by looking at the parts of these rational functions. It isn't like the equation of a line, (linear function), f(x) = mx +b, where you just have slope and intercept to worry about. At first, rational functions seem wildly complicated. This example is a question about interpreting the parts of expressions.


 0 kommentar(er)
0 kommentar(er)
